Given a set of candidate numbers \(C\) and a target number \(T\), find all unique combinations in \(C\) where the candidate numbers sums to \(T\).
The same repeated number may be chosen from \(C\) unlimited number of times.
Note:
- All numbers (including target) will be positive integers.
- Elements in a combination (\(a_1, a_2, \cdots , a_k\)) must be in non-descending order. (ie, \(a_1 \leq a_2 \leq \cdots ≤ a_k\)).
- The solution set must not contain duplicate combinations.
For example, given candidate set 2,3,6,7 and target 7,
a solution set is: [7]
[2, 2, 3]
The popular solution is to recursively scan all elements in the cadidate set, such as http://yucoding.blogspot.com/2012/12/leetcode-question-16-combination-sum.html.
However, I don’t want to use recursion. My solution to this problem is to build trees level by level for each number in the candidate set, where the nodes are candidate set number. The sum of the sequence from root to current node is compared to the target:
- if the sum equals to the target, then we find one solution;
- if the sum is less than the target, then subnodes could be added to this node;
- if the sum is larger than the target, then this node is a leaf node.
Only numbers equal to or larger than current node can be used as the children of current node. When there is no child could be added, this tree stops growing.
For example, given candidate set, \({2,3,6,7}\) and target 7, the following trees could be built:
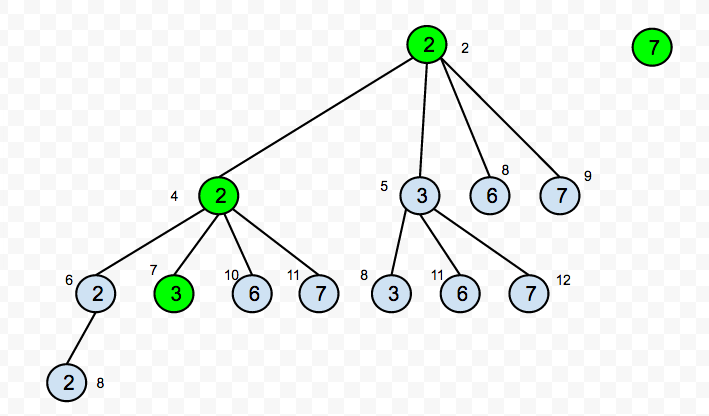
Based on above strategy, my C++ implementation is:
class Solution {
public:
struct Node {
int val;
int sum; // sum to now
vector path; // path to now
//Node* pre; // parent node
};
vector<vector > combinationSum(vector &candidates, int target) {
vector<vector > trace;
for(auto& x:candidates) {
if(x==target) {
vector tr={x};
trace.push_back(tr);
continue;
}
// Build trees in level order for every candidate
vector<vector> layers;
int cur=0;
int next=1;
vector tmp;
layers.push_back(tmp);
layers.push_back(tmp);
Node nd={x,x,{x}};
layers[cur].push_back(nd);
while(layers[cur].size()>0) {
for(auto& y:layers[cur]) {
for(auto& z: candidates) {
if(z>=y.val && z+y.sum<=target) {
Node tmp_nd;
tmp_nd.val=z;
tmp_nd.sum=z+y.sum;
tmp_nd.path=y.path;
tmp_nd.path.push_back(z);
if(tmp_nd.sum==target) // reach the target, record the trace
trace.push_back(tmp_nd.path);
else
layers[next].push_back(tmp_nd);
}
} // end for z
} // end for y
cur=!cur;
next=!next;
layers[next].clear();
//cout<<endl;; // TEST ONLY
} // end while
}// end for
return trace;
}
};
</pre>