This is the second article on binary tree operations. For other topics on binary tree, please refer to
- Binary Tree Operations(I)
- Binary Tree Operations(II)
- Binary Tree Operations(III) - Convert a Binary Tree to Down-Right Representation
- Binary Tree Operations(IV) - Determine if a Binary Tree is a Binary Search Tree
1. Path Sum
The Path Sum problem of binary tree is:
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
This problem can be easily solved by level-order traversal. During traversal, record the sum and path to each node:
- if the sum to current node is larger than the given sum, then remove the sum and path to current node and stop tracing its child nodes.
- if the sum to current node equals to the given sum, the print or record the path.
- if to current node is less than the given sum, continue searching its children.
For the source code of this section, please refer to function PathSum() in my Binary Tree Library.
2. Build Binary Tree With Cycle
To build a binary tree with cycles, we can first build a binary tree using the method described in Binary Tree Operations(I), and then add links between two nodes. However, we need to keep in mind that we are dealing with binary tree, so for each node, there are at most two children(left and right).
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
For example, given a binary tree in following image,
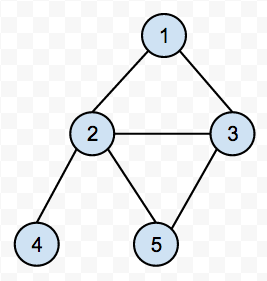
We can build a tree using string sequence {1,2,3,4,#,5,#} at first, and then add links {3->2, 2->5}. Or build tree {1,2,3,4,5,#,#} first and then add links {3->2,3->5}.
For the source code of this section, please refer to functions BuildTree() and BuildCycleTree() in my Binary Tree Library.
3. Detect Cycle in Binary Tree
Cycles in a binary tree can be detected by DFS(in preorder) - if there’s a cycle, there must be a node has a child node that is already been accessed before(i.e. a right hand node linked to the left hand node). A unordered_set can be used to record the nodes that have been accessed.
Considering above example again, when we traverse that binary tree in pre-order, we would first access nodes {1,2,4,5}. And when we accessing node 3, we will find that node 3 has a child 2(or5) that has already been accessed. So this tree has a cycle.
For the source code of this section, please refer to function HasLoop() in my Binary Tree Library.